Всем механикам с юности памятна картинка со схемой движения автомобиля по кривой, когда его внешние колеса проходят больший путь, чем внутренние. С ее помощью во многих учебниках для водителей разъясняются назначение и принцип действия дифференциала. Часто все сводится к тому, что дифференциал позволяет ведущим колесам вращаться с различными скоростями и, таким образом, обеспечивает нормальное движение автомобиля на поворотах.
Такие разъяснения не то чтобы совсем неправильны, но слишком упрощены и сути работы дифференциала не раскрывают. Конечно, в серьезных книгах все изложено правильно. Там сказано, что назначение межколесного дифференциала на автомобиле состоит в распределении крутящего момента строго поровну между ведущими колесами одного моста, а межмостового дифференциала – в распределении крутящего момента между ведущими мостами, — поровну или в оптимальной пропорции (несимметричный дифференциал).
Эту ситуацию можно считать вполне допустимой для водительских учебников и для популярной литературы, пока объяснения просто не полны и ограничиваются фразами типа:
«Дифференциал – это механизм, у которого ведущие колеса вращаются независимо друг от дружки».
Строго говоря, вращаются они «зависимо», ну да ладно, — что-то похожее на правду сказано, а об остальном ни слова, чтобы не забивать голову людям без специальной подготовки.
Хуже, когда авторы, тиражируют свое неправильное понимание сути работы механизма, как это сделано, например, в книге:
Зеленин С.Ф., Молоков В.А. Учебник по устройству автомобиля, М., «Русьавтокнига», 2000 г., 80 с. Тираж 15000 экз.
Цитата из этой книги:
«Дифференциал предназначен для распределения крутящего момента между полуосями ведущих колес при повороте автомобиля и при движении по неровностям дороги. Дифференциал позволяет колесам вращаться с разной угловой скоростью и проходить неодинаковый путь без проскальзывания относительно покрытия дороги.
Иными словами 100% крутящего момента, который приходит на дифференциал, могут распределяться между ведущими колесами как 50 х 50, так и в другой пропорции (например, 60 х 40). К сожалению, пропорция может быть и 100 х 0. Это означает, что одно из колес стоит на месте (в яме), а другое в это время буксует (по сырой земле, глине, снегу).
Что поделаешь! Ничто не бывает абсолютно правильным и идеальным, зато данная конструкция позволяет автомобилю поворачивать без заноса, а водителю не менять каждый день напрочь изношенные шины.
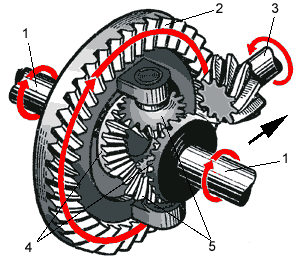
Рис. 38 Главная передача с дифференциалом
1 — полуоси; 2 — ведомая шестерня; 3 — ведущая шестерня; 4 — шестерни полуосей; 5 — шестерни-сателиты
Это уже не упрощение, а просто введение в заблуждение читателей. Здесь, кроме второго предложения и иллюстрации, все неправда (в первом предложении нужно вставить слово «поровну», а точку поставить после слова «колес» и т.д.).
Только однажды в учебнике для профтехобразования мне довелось встретить правильное и при этом простое и наглядное разъяснение сути работы дифференциала. Было это давно и помню только, что это был учебник для водителей зерновых комбайнов.
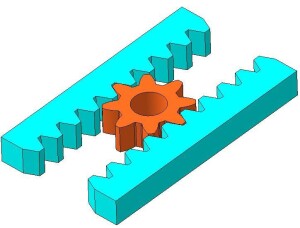
Там читателю предлагалось вообразить, что две полуосевые конические шестерни «развернуты» в две зубчатые рейки, эти рейки лежат на воображаемом столе, а между ними помещен сателлит в виде прямозубой шестерни. Выглядит это примерно так:
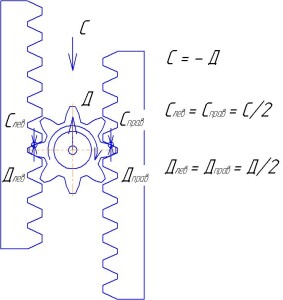
Объяснение сути работы дифференциала основано на его конструкции и на третьем законе Ньютона, который гласит: сила действия равна по модулю и противоположна по направлению силе противодействия. На следующем рисунке показано силовое взаимодействие сателлита с рейками, когда движущая сила Д приложена к оси сателлита и этот сателлит толкает обе рейки по столу, причем силы сопротивления движению левой и правой реек Слев и Справ одинаковы (силы трения реек о поверхность воображаемого стола) и каждая из них равна половине общей силы сопротивления С. Силы со стороны сателлита передаются на рейки в точках зацепления зубьев сателлита с зубьями реек. Благодаря равенству сил сопротивления движению Слев и Справ, равны между собой и движущие силы на зубьях сателлита, каждая из которых равна половине движущей силы Д. Поскольку равные силы приложены к двум зубьям сателлита, находящимся на равных расстояниях от его оси, сателлит находится в равновесии и не вращается. Поэтому все три детали движутся прямолинейно в одну сторону и с равными скоростями, а именно с той скоростью, с какой движется ось сателлита и которая задана двигателем.
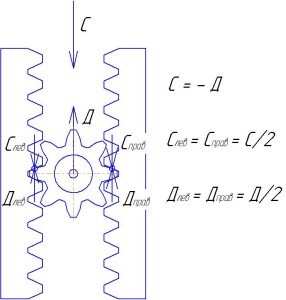
Эта ситуация соответствует установившемуся движению автомобиля по дороге с хорошим сцеплением с дорогой.
Теперь представим, что при своем движении по столу, левая рейка «наехала» на пятно масла. При этом сила сопротивления ее движению (сила трения о стол) уменьшилась, а сила сопротивления движению правой рейки осталась прежней. На какой-то момент равновесие сил на зубьях сателлита нарушается: нагрузка на левый его зуб становится меньше нагрузки, действующей на его правый зуб. Иначе говоря, сателлиту стало легче толкать левую рейку, чем правую. Поэтому он начинает вращаться по часовой стрелке, как это показано на следующем рисунке.
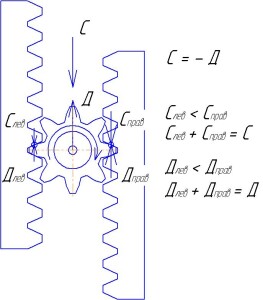
вращению сателлита движение правой рейки замедляется, а левая рейка наоборот ускоряется. Затем правая рейка полностью останавливается, а сателлит продолжает вращаться. Его ось продолжает двигаться с той же скоростью, что и прежде, так как эта скорость задана двигателем. Но поскольку правая рейка стоит, вращающийся сателлит обкатывается по ней. В момент, показанный на рисунке правый зуб сателлита стоит на месте, так как «упирается» в зуб неподвижной рейки. Но противоположный, левый зуб сателлита движется в два раза быстрее, чем ось самого сателлита. Все это соответствует ситуации, когда одно из ведущих колес медленно движущегося автомобиля наезжает, например, на обширное пятно льда, а второе остается на сухом покрытии с хорошим сцеплением. То есть машина останавливается и колесо, находящееся на льду, буксует, вращаясь в два раза быстрее, чем прежде, когда оба колеса катились с одинаковой скоростью.
Строго говоря, о нарушении равновесия сил на зубьях сателлита выше сказано некорректно и только потому, что, как мне кажется, так проще понять происходящее. На самом деле равновесие сил сохраняется всегда, только для его рассмотрения нужно еще учитывать силы, вызывающие ускорение левой рейки и замедление правой. Эти не рассматриваемые нами силы, исчезают с момента полной остановки правой рейки. В этот же момент удвоенная скорость движения левой рейки становится постоянной. И тогда ситуация полностью соответствует следующему рисунку.
Здесь равновесие сил восстановилось, точнее, — исчезли динамические силовые составляющие (те, что вызывали ускорение одной рейки и замедление другой). Правая рейка стоит, сателлит вращается, а левая рейка движется равномерно с удвоенной скоростью. Очень важно отметить что, равновесие сил перешло на новый уровень. Теперь равные силы на левом и правом зубьях сателлита стали существенно меньше прежних. В силу третьего закона Ньютона эти силы не могут превысить движущую силу, которую можно приложить к рейке, находящейся на пятне масла, или к колесу, находящемуся на пятне льда. Иными словами, если одно колесо стоит на сухой дороге, а противоположное буксует на льду или в грязи, это вовсе не означает, что 100% крутящего момента передается от двигателя на буксующее колесо, как сказано в упомянутой выше книге. Этот момент всегда и во всех условиях делится дифференциалом поровну между колесами, но он не может быть больше, чем позволяет сцепление одного из колес с дорогой, причем именно того колеса, у которого это сцепление меньше.
Только если в этих условиях заблокировать дифференциал, то есть выключить его из работы, тем или иным способом жестко соединив между собой полуоси, можно передать на колесо, стоящее на сухой дороге, подавляющую часть крутящего момента, который может развить двигатель. При этом буксование прекратится, оба колеса будут вращаться с одинаковой скоростью, но подавляющую часть суммарной силы тяги будет обеспечивать только одно из этих колес.
Мне кажется, что с помощью модели с зубчатыми рейками можно наглядно объяснить и все прочие режимы работы межколесного дифференциала. Например, ситуацию, иногда возникающую при торможении двигателем. Представим, что автомобиль движется под уклон на сухой дороге с пятнами льда. Водитель тормозит двигателем. В этом случае движущая сила, это сила инерции массы машины. А сила сопротивления движению, это сила, приложенная к осям сателлитов дифференциала со стороны двигателя. Одно из колес наезжает на пятно льда. Сила сцепления этого колеса с дорогой резко уменьшается, и оно начинает вращаться в обратную сторону. Здесь происходит то же самое, что произойдет с рейками если ось сателлита сделать неподвижной, но оставить ему свободу вращения вокруг этой оси, то есть имитировать ситуацию, когда ось сателлита тормозится или удерживается двигателем. Если теперь двинуть вперед одну из зубчатых реек, то сателлит начнет вращаться и заставит вторую рейку двигаться назад. Здесь рейка, движимая вперед, соответствует колесу на сухой дороге, а рейка, движущаяся назад, — колесу, находящемуся на льду и вращающемуся в обратную сторону. На мой взгляд, вращение буксующего колеса в обратную сторону очень наглядно демонстрирует «стремление» дифференциала выполнить свое предназначение и выровнять силы на двух колесах ведущего моста. В данном случае это силы торможения. Благодаря их выравниваю исключается или сильно снижается вероятность заноса автомобиля при таком режиме торможения.
Можно рассматривать еще многие ситуации, возникающие при работе дифференциала. Но полагаю, что и сказанного достаточно, чтобы убедиться: — межколесный дифференциал всегда делит получаемый от двигателя крутящий момент поровну между двумя колесами одного ведущего моста.
А теперь вернемся к упомянутой в самом начале картинке с автомобилем, движущемся по кривой. Если автомобиль заднеприводной, то получающие одинаковый крутящий момент два задних колеса преобразуют эти крутящие моменты в две одинаковые силы тяги (если шины колес имеют одинаковый диаметр, одинаковое давление накачки и несут одинаковые части веса автомобиля). А две одинаковые силы тяги стремятся толкать автомобиль по прямой. Именно поэтому, водителю при прохождении поворота приходится твердо удерживать рулевое колесо. Строго говоря, дифференциал на таком автомобиле не столько помогает, сколько мешает прохождению поворота. Зато он прямо способствует устойчивости движения по прямой (вместе с углами установки передних колес).
У переднеприводного автомобиля ситуация несколько иная. Здесь силы тяги также одинаковы на двух колесах, но они «поворачиваются» вместе с поворачиваемыми колесами. Поэтому, например, переднеприводной машине легче выйти из глубокой скользкой колеи: повернутые передние ведущие колеса активно тянут куда нужно. А у заднеприводного, задние ведущие колеса активно толкают машину вдоль колеи.
Здесь рассмотрена лишь малая часть того, что следовало бы водителям знать о работе дифференциала и на это потребовалось много слов и картинок. Так может быть правы те, кто ограничивается пресловутой картинкой с разным пробегом у разных колес на повороте? Может быть. Но полагаю, что следует, если и не вдаваться в пространные разъяснения, то хотя бы просто написать, для чего действительно предназначен этот механизм. А кто захочет дойти до сути, найдет, где об этом почитать. И уж совсем ни к чему пропагандировать собственное неверное понимание этой сути.
Д.Д.